Reply with anything

[_Chilling_]

Just reply with anything u feel like


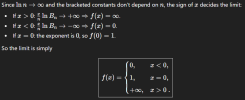
The given function is

f(x)=limn→∞(x+nn)(n!(x2+n2)(x2+n24)...(x2+n2n2))x/nf of x equals limit over n right arrow infinity of open paren the fraction with numerator x plus n and denominator n end-fraction close paren open paren the fraction with numerator n exclamation mark and denominator open paren x squared plus n squared close paren open paren x squared plus the fraction with numerator n squared and denominator 4 end-fraction close paren point point point open paren x squared plus the fraction with numerator n squared and denominator n squared end-fraction close paren end-fraction close paren raised to the x / n power

 

[Meth0vas]

Get rid of n! because it makes all easier. Also lim n goes -infinite and not +infinite (i dont know but people think i know hehehe)
And you could do 2x or 24n instead of x2 or n24

 

[Bumbrah]

I hate math

 

[Meth0vas]

Basically if f(x) = 0, x=<0. If f(x) = 1 then x would be 0. But if f(x) = +∞ the x would be positive...
At least thats what Artificial Intelligence said: